Gotcha w/comparing base64 encoded strs
Here’s a fun experiment - consider two “numerical” strings such as:
a = "1004"
b = "1053"Is a < b?
Why yes, of course it is!
Ok, let’s try this again, this time b64encoding our two strings.
import base64
a_b64 = base64.b64encode(a.encode("utf8")).decode("utf8")
# MTAwNA==
b_b64 = base64.b64encode(b.encode("utf8")).decode("utf8")
# MTA1Mw==How about now?
Is a_b64 < b_b64?
NOPE.
What gives?!
And more importantly, this observation implies that:
Given two strings a, b such that
a < bit is not necessarily true thatb64(a) < b64(b)!
(This is the key takeaway, the rest of this post explains why this is true for some cases)
But why though?
To answer this question, we must delve into the b64 encoding algorithm itself. Let’s consider 1004 as an example.
Step 1: split the string by digit
| 1004 |
|---|
| 1 |
| 0 |
| 0 |
| 4 |
Step 2: convert each char to binary equivalent in ASCII
| 1004 | ASCII value | Binary |
|---|---|---|
| 1 | 49 | 00110001 |
| 0 | 48 | 00110000 |
| 0 | 48 | 00110000 |
| 4 | 52 | 00110100 |
Step 3: concatenate the binary representation
1004=>00110001001100000011000000110100
Step 4: partition the above but now in groups 6
| 1004 (in groups of 6) |
|---|
| 001100 |
| 010011 |
| 000000 |
| 110000 |
| 001101 |
| 000000 (pad 4 to complete final group |
Step 5: pad-left each partition to convert our 6 bit “byte” into an 8 bit byte
| 1004 |
|---|
| 00001100 |
| 00010011 |
| 00000000 |
| 00110000 |
| 00001101 |
| 00000000 |
Step 6: convert back to decimal (base 10) and translate by looking up each decimal value in the base64 characters table
| 1004 | decimal | b64 character |
|---|---|---|
| 00001100 | 12 | M |
| 00010011 | 19 | T |
| 00000000 | 0 | A |
| 00110000 | 48 | w |
| 00001101 | 13 | N |
| 00000000 | 0 | A |
So,
1004=>MTAwNA
Tada!
Now (do try this at home, if you want): repeat this exercise for 1053, resulting in:
1053=>MTA1Mw
Note that MTAwNA > MTA1Mw.
The key to understanding why b64(a) !< b64(b) has to do with Step 6.
We convert our new, transformed decimal values according to the base64 characters table - which places numbers such as 1-9 as higher than characters (in terms of index value).
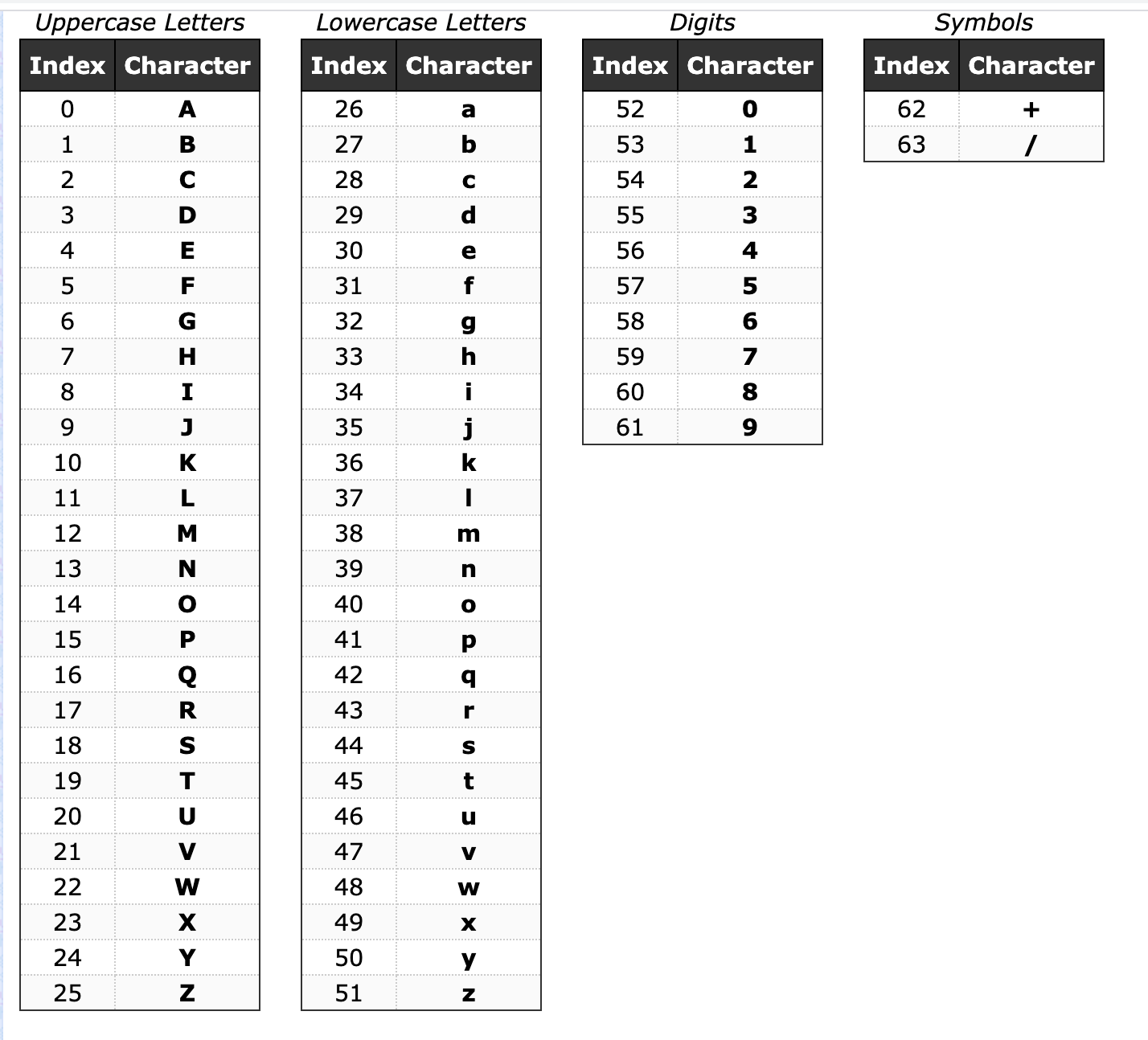
Notice how 1 has decimal value 53 and w has decimal value 48. Contrast this to the ASCII table:
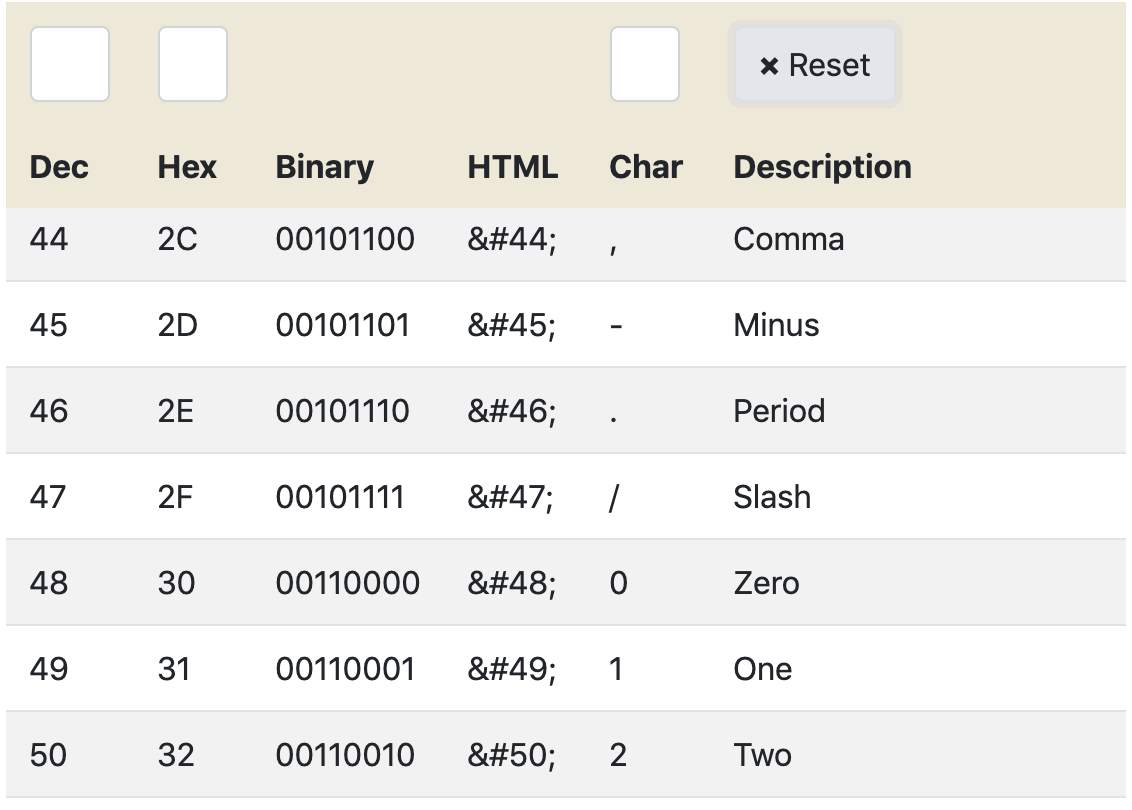
Note that "1" has a decimal value of 49.
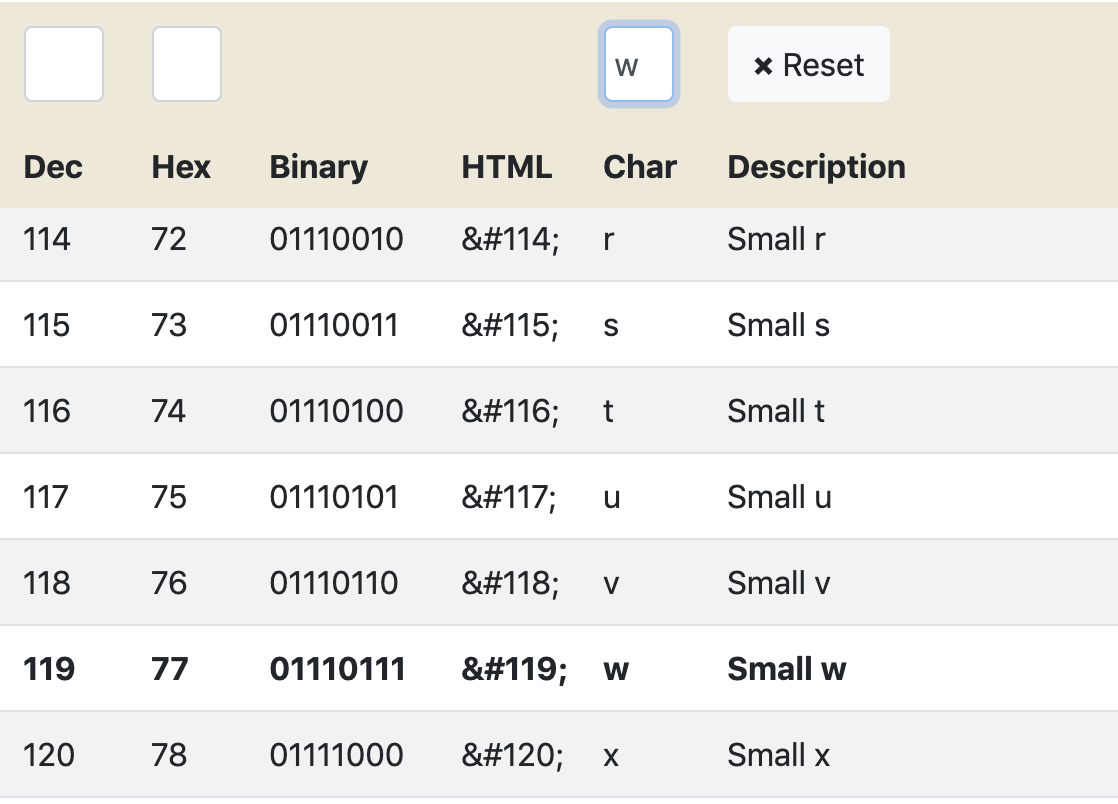
But "w" has a decimal value of 77!
So, when comparing "w" > "1" as strings, the expression is evaluated as True!
In other words, when we convert our bits from Step 4 to characters, we splice the binary representation because our total # of bits is not divisible by 6 (see my PPS for more info).
Then we convert this spliced value in our b64 table where the numeric chars (1-9) have indices that are higher than the indices of the non-numeric chars (A-Z and a-z).
For this reason, when we attempt to perform a string compare, 1004 in b64 encoded form (MTAwNA) is indeed less than 1053 in b64 encoded form (MTA1Mw) according to the rules of b64 translation but not according to the ASCII translation (see my PS for more info).
In ASCII format, MTAwNA is indeed “greater” than MTA1Mw since char position 3 in MTAwNA (w) actually has a numerical index that is higher than char position 3 in MTA1Mw (1).
Womp womp.
Ok but…why care about this?
Well, long story short: friends don’t let friends take fields in their elasticsearch index, b64 encode them into a key and then run queries sorting by these keys because well…it won’t work.
I had one hell of a time figuring this out and even when I observed it, I had trouble justifying this to myself hence this post (which I used to work out my feelings on the matter).
I feel slightly better now.
PS: in py3 we compare unicode values not ascii when performing string comparison ops - but for the purposes of this post the decimal values are the same since we are only contending with A-Z, a-z,0-9,+,/
PPS: 8N mod 6 will always have remainder 2, 4, or 0. This problem seems to show up specifically when (8N mod 6) == 2 (ie: we pad 4 0s to the right of our last row). The mod 0 case is obvious but I’ve yet to explain why (8N mod 6) == 4 does not seem to this problem.